株のバリュエーションというもの by yamamoto
4月10日に初めて出光(5019)に取材に行く。
そこで、こういうタイプの会社の株価の評価について、少し、考察する。
こういうタイプとは、バランスシートで商売をするタイプということで、おしなべてPERなどの伝統的株価指標は低いという特徴がある。
バリュエーションとは?
金融商品の価値を評価することをバリュエーションという。
たとえば、いま手元にある現金1万円札。この価値は、一万円である。
ただし、明治時代の1円はいまの1円ではないことからわかるように、通常はインフレのため、将来の現金価値と現在の現金価値とは違う価値となる。
いまの1万円を投資に回せば1年後には1万円を超える価値が手に入ることは誰にでもわかるだろう。
1年の定期預金が0.1%であれば、銀行に一年寝かせておく。すると、1年後には10010円になる。
だから、1年後の10010円といまの10000円とは同じ価値だと見なす。
こうした預金や債券がほぼ確定的なのに対して、株などのリスク資産は、だれにも1年後の適正な価値がわからない。
この不確実性から、リスクを推定して、将来と今の価値の橋渡しをする。
それではそれはどうやってするべきなのか。
株のバリュエーション
1年後に今の株価の2%程度の配当を予定している株があるとしよう。
すると、いま10000円でこの株を買えば、1年後には10200円になると見るのが普通の見方だ。
預金と比べて断然リターンは高い。だが、世の中を見渡してみて、預金をする人が大多数で株に投資している人は少数派だ。
なぜならば、預金は約束であるのに、配当は単なる権利にすぎないからだ。「会社の業績が見通し通りならば」という条件付きの権利にすぎない。
それでも、配当の変動率は過去の推移からわかる。
たとえば、出光の場合、過去10年の配当成長率は8%程度。その標準偏差は18%程度である。
仮に、過去の変動率がそのまま将来の変動率を表すとする。
過去は将来ではない。過去の動きから、将来の動きなぞわからない。
そうはいっても、たとえば、ものすごく頭のよい人をあなたが知っていて、仮に彼を山田くんとしようか。その山田くんが10年後にあったときに、とても、とてもおバカさんになっている、という見通しは立てにくいだろう。
頭がよい人が将来、とてつもなくバカになる可能性が低いのと同様に、過去順調だった事業が将来まったくダメになることもあまりない、と考えるわけだ。
つまり、わたしたちは、過去から将来を推し量るしかないのだ。投資家のやるべきことのひとつは、企業の過去を整理し、分析することなのだから。
さて、出光の配当の変動率の期待値が年率8%成長で、その標準偏差が18%であるとする。
期待値は時間に比例するがリスクは時間の平方根に比例する
年率の8%成長とは、10年後には連続複利ベースで2.2倍になる。(exp(0.8×10)=2.22)
ところが、10年間の変動率の標準偏差は18%のルート10倍にすぎない。
計算すれば、exp(0.18 x 10^0.5 ) = 1.76なので10年間のリスクは1年間の1.76倍でしかない。
10年後の配当の期待値は現在の80円配当の2.2倍だから、176円である。
だから、出光株の10年後の将来の価値は、現状の東証1部の平均配当が2%程度だから、176/0.02=8800円となる。
この8800円は10年後にもっともありえそうな配当水準をいまの市場平均で評価したものである。なぜ10年後の市場平均で評価しないかという方がいらっしゃったら、その通り。いまの市場評価で評価するために、現在価値に引き戻すわけだ。
これまで、ファイナンスの教科書では、年率のリスクをそのまま年率で引き戻して、たとえば7%程度をリスクプレミアムとする場合が多い。
わたしはその立場を取らない。
リスクとリターンとはまったく違う概念であり、リスクは時間の平方根に比例し、リターンは時間比例だという考えをもっている。
なぜならば、たとえば日経平均のリスクは年率2割だとしよう。そのとき、30年間のリスクは2割の30倍になるだろうか。つまり、株の変動率は30年で600%といえるだろうか。そして変動率の平均値を5%としよう。
連続複利でさえ、マイナス600%は、ほぼ元本ゼロとなってしまう。
業績の予想がそれるリスクを標準偏差で代替するならば、リスクは時間の平方根に比例するとするしかないのである。たとえば、20%のリスクを30年の平方根で割り引けば(exp(-0.20 x 30-0.5)) =0.33となる。
30年後の日経平均は、いまの4.5倍程度になっていて(5%成長で30年だから)、10万円。
だが、16%程度の確率で3万円以下。84%以上の確率で3万円以上、16%の確率で17万円以上、という感じと見るのだ。
つまり、期待値10万円±7万円と見るということだ。
これを十中八九の不利な方に、1σ分の悪い状況(確率16%)が起こると想定して、
exp(5% x 30)exp(-20% x 30^0.5) x いまの株価 =32000円を将来の日経平均の期待値を1σのリスクで「割り引いた」価値と見なすことができる。
これは現在価値ではない。
が、将来の価値の期待値に対するシナリオの1σ分のリスクを割り引いた将来価値である。
将来、まあ、十中一二、まあまあ悪いことが起こるという考え。ツキがないときであっても、いまの2万1500円から下回ることはないぞ、という考え。
将来がどんなに悪くても、継続した努力を続けるならば、今よりはずっとよい!という考え、これがわたしのバリュエーションの基本的な考え方である。
なぜ、こう考えるかというと、人は未来を切り開いているものであるかぎり、人口減だとか大災害とかを乗り越えて、わたしたちは集団として、地道な成果をあげることができるんだという決意である。
努力している人が努力している人がわかり、成長志向の人は成長志向の企業がわかる。
努力してリスクをとる人がリターンを得るんだ、そうでなければ努力は報われないという投資宗教のようなものである。
リスクプレミアム7%で30年間割り引くとほぼゼロになる
投資におけるバリュエーションの前提は、少し先の未来に期待できるキャッシュフローをゼロと評価していることが基本である。
これまでは金利がある程度の水準であった。その金利は無リスクと見られていたから、伝統的に株式のリスクは7%とか6%程度と置かなければならないとされてきたのだ。
いま、無リスク資産の金利がほぼゼロの時代である。
ゼロ金利というこの時代特有の新しい考えがどうしても必要になるのではないかなあ。
リスク資産である株価の動きから推定する
株価そのものを分析することで、リスクを推し量ることができる。
つまり、出光の株価の変動率を上場来で平均して、その標準偏差を求めてみよう。
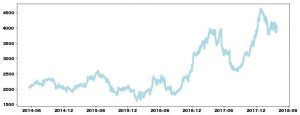
変動率の平均を期待値として、それはほぼゼロ。標準偏差は30%程度だ。
そうなると、やはり、リスクは年間で30%程度ある、としなければならない。
出光の今の配当は80円で配当利回り3%程度だから、配当成長率ゼロとするならば、現状の株価は3割ほど割高という結論になる。これは1年後の配当を3割で割り引くとそうなるわけだ。
会計のブレから計算する
出光のようにバランスシートを使うビジネスについては、純資産が毀損するリスクがあるため、評価は低くなる。
事業においてバランスシートを使うと評価が低くなるのは、在庫リスクが大きいからだ。
たとえば、銀行や商社はバランスシートをフルに使うので、貸し出しや商品の価値が下がると大きな損失を被る。
出光の場合、5000億円程度の在庫があって、この在庫が商品市場でおよそ3割の年率変動率の標準偏差を持つ原油だとしよう。すると、3割のリスクは1500億円となって、これは自己資本8400億円の17%を占めてしまう。
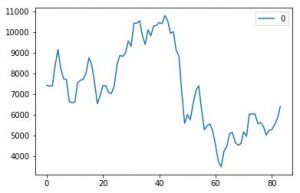
(円ベースの原油価格の推移)
つまり、純資産が17%毀損するシナリオが確率でいえば10中1−2回起こる、ということだ。
これが直接、減配圧力になると厳しくみなせば、割引率は17%程度で見なければならないということだ。
(実際は、そんなことは起こりようがない。スライド性を取る限り、仕入れ値が売値に反映される。在庫が2ヶ月だとすれば、17%の毀損の確率は極僅かなはずである。コモディティバブル崩壊で原油が半値以下になり、最終赤字に陥ったときも低い配当性向もあり、出光は配当を維持した。株主資本の毀損と減配可能性とはイコールではない。)
一方で、 現状ROE18%で配当性向が非常に低いことを考えると、配当成長率はやはり18%近くある、ということも同時にいえる。
つまり、成長率とリスクが見合っている状況であり、80円の配当の1年後の見通しは、やはり、80円ということになる。配当利回りを市場並みの2%で評価するならば、いまの株価は妥当な水準ということになる。
2段階DDMモデル
2段階DDMモデルで評価すると、今後10年の出光の配当成長率を15%とし、リスクを15%する。
将来の出光の配当は連続複利で15%増えていく。同時に将来の出光の配当がぶれるリスクは時間の平方根で増えていくとする。すると、将来価値はいまの株価よりも随分と高くなる。配当の将来の期待値の1σ下の下振れリスク折り込みの期待値はいまの配当の2.8倍だ。(exp(0.15×10-0.15×10^0.5)=2.8)
もちろん、これは将来価値でシナリオが崩れたときの見通しであるから、これ以上の成果は存分に期待できる。
市場平均で配当を評価する、と再三、書いているが、そう書くのは、平均への回帰という考え方に則っているからである。
(この考え方を使わないと計算できないから使っているにすぎない。10年という短い期間における平均への回帰をわたしは信じていない)
アクティブ運用者の場合、アナリスト予想期間を第一ステージ、平均への回帰期間を第二ステージとして、第三スレージに平均的な会社となる、と予想する。その場合、本質的な価値は、第三ステージの配当水準を「どう割り引くか」の問題と同じである。たとえ第1ステージが10年、第2ステージが10年ならば、20年後のリスクとリターンを予想するということになる。この場合は、三段階DDMである。
2段階DDMは、ROEが高い会社にとっての評価はより厳しくなる。第一段階はアナリスト予想期間。その後すぐに平均への回帰が起こると想定する。
ファイナンスの教科書に書いてあるDDMは一段階のDDMであり、これは実務上、全く使い物にならない。証券アナリストなら誰も知っているP = d/(r-g)という式で表現されるものだ。役に立たないのは、永久成長率gを設定しなければならないからであり、そんなもん、わかるわけないだろ!で一喝されておしまいになる代物にすぎない。特に成長株投資家は予想期間においてROEの高い会社の業績を予想するため、g>rであるのが普通だ。そういうこともあって、多段階のDDMが現場で使われてる背景になっている。単純な一段階DDMはまったく使われていない。
2段階であっても3段階であっても、アナリスト予想期間と成長率の見通しとリスクの考え方で、価値は人それぞれに大きくぶれてしまう。アナリストによって、ある銘柄が買いなのに、別のアナリストが評価したら、中立になる、ということは結構ある。(だから相場は面白い)
わたしの場合は、2段階モデルを使うが、評価するのは、将来価値のbad caseが今の価値と比べてどうなのかという判断になる。これは前述の通りだ。無リスク金利がゼロという特殊?な事情があるので、そうしている。
成長株は長期持てばキャッシュより有利である
インデックス投資家というものがいる。彼らは長期の投資を念頭にわずかなコストも長期では大きな差になることをわかっている合理的な人々だ。
株式投資家は、大きなリターンの差を長期にわたり享受できるため、リターンはインデックス投資家の数十倍、数百倍になる。だが、将来のシナリオのリスクは10倍にもならないだろう。
リスクとリターンの比は、時間の経過とともに、投資家に有利になる。金利ゼロが続くならば。
ただし、配当の成長が期待できる企業についてだけだ。
それでは今回の出光はどうなのか。
これまで見てきた通り、ROEが2割近くあり、過去の配当の成長率の実績が二桁近いということを考えると、配当成長率の期待値は10桁程度はあるだろう。
それは、すなわち、成長株といえる。成熟株とはROEが低い株、成長株とはROEが高い株とするならば、出光の現状はROEが高い部類であるといわざるをえない。
すなわち、その事業リスクの高さに関わらず、リターンの見通しがプラスであるならば、持てば持つほどシャープレシオは向上していく、というわけだ。
バリュエーションにはいろいろな考え方がある。投資家は自分なりにいろいろと自分だけのバリュエーションを考えるものである。そういう多様なバリエーションの考え方があって、市場の売り買いが成立しているのである。
企業というものは、事業を営む主体であり、事業からの期待値はプラスに決まっている。そして、事業からの利益は再投資されていく。事業環境によっては追い風もあり、向かい風もある。
いわば、エンジン付きの車に投資家は乗っているのである。このエンジンの強さがROEの高さといってよいだろう。
前に進みたいが、向かい風があまりにも強いと、バックしてしまうこともある、ということだ。だが、大抵の場合、速度は保証できはしないが、前に進んでいくことぐらいなら10中8−9、前には進むものである。
10中8−9、前に進む、リターンがプラスであるのだから、自分の好きなエンジンを選べばよい。
10個から50個ぐらいのエンジンを選べば、前に確実に進む。たくさんのエンジンでほぼ確実に前に進むことは、ポートフォリオ理論を勉強すればわかることである。
まとめ
ゼロ金利の長期化で、預金の将来価値の魅力が昔に比べて落ちてしまった。
長期の時間を利用しよう。コツコツを長期的に努力する企業は長期で報われるはずだ。
配当の将来価値、株価を年率のリスクプレミアムで現在価値に割り引くのではなくて、
将来の見通しのbad シナリオとして将来価値を期待値プラスマイナス1σで評価しよう。
そのとき、配当変動率の期待値が大きなプラスならば、長期保有は絶対に有利だ。
将来価値を信じて投資をする。合理的に投資をする。バッドシナリオも用意をしておく。
長期投資とは、複利効果を体現するために、時間を犠牲にする投資ではある。だが、継続はちからなりというではないか。時間を味方にして、複利の力をあてにしつつ、信じる企業を応援するしかない。
(仮に無リスク資産の長期金利が5%ならば、現在価値への割引率も5%を超える水準で設定しなければならない。)
補足: 連続複利とは? 連続複利の勧め
投資理論、つまり、バリエーションを算定するためには、連続複利を使うべきである。
連続複利 r とは、5年間で株価が3倍なったら、r = 5^-1 x Log e 3 で表されるものである。(自然対数)
https://ja.wikipedia.org/wiki/%E8%87%AA%E7%84%B6%E5%AF%BE%E6%95%B0
年複利rで5年運用すれば結果は(1+r)^5倍になる。
連続複利rで5年運用すればexp(5x r)倍になる。(ネイピア数の指数関数)
https://ja.wikipedia.org/wiki/%E3%83%8D%E3%82%A4%E3%83%94%E3%82%A2%E6%95%B0
よく、投資家の中には、相場の下落の怖さを表すときに、50%下がって50%あがっても100%には戻らない。だから、下げに対しては特別に対応しなければならない、云々という議論をする人がいる。
こういう議論は確かに単利と複利の混同から起こる。
単利は当初の元本を1として、それがどうなるかを見る指標である。単利で+50%ならば、1が1.5になるので明快だ。これが連続複利の50%はexp(0.5)=1.64…となり1.5にはならない。こういう明快さから普段の生活では単利で話すことが圧倒的だ。
50%上がって50%下がれば75%になる、という人の議論は、1.5の0.5倍は0.75である、というわけだ。掛け算は順番を入れ替えても結果は同じだから、0.5倍の1.5倍も0.75になる。
だが、単利の精神とは、当初の元本を1として物事を測りましょう!というものであるから、この上記の議論は、単利をパーツとして用いながら、複利をやってしまっている、という意味で二つの概念を混同した議論である。1.5倍が半値になった、あるいは。半値から1.5倍になった、というのは、途中で元本を取り替えてしまっている。1のはずの元本が0.5の元本や1.5の元本に取り替えられてしまったのである。
これはいけない。単利で表現するならば、1に対して、50%増えたが、次に、最初の1に対して、75%減ってしまったというべきなのだ。(1+0.5ー0.75) あるいは、最初の1に対して50%減ったが、その1に対して、次に25%増えたというべきなのだ。(1−0.5+0.25)
このように、単利を時間概念を消し去って使う場合があるが、フィナンシャルの世界では、単位時間をつかって、投資成果の優劣を測る。50%減る、にしても、それが10年で50%減ったのか、あるいは、1週間で減ったのか、では投資の優劣が違う。
単利の議論では株価がゼロ以下になってしまうことが起こりうるのである。単利で200%やられる場合は、1−2=−1となって、元本相当が借金になることをいう。
だが、現象として、株価がゼロ未満になることはない。投資は有限責任であるであるから。
(株価は負にならないが、投資成果は、レバレッジを使えば、経済効果として負の値になることは大いにある。)
連続複利は、バリュエーションをしっかりと計算するためにどうしても必要なものであり、
連続複利は元本を取り替えならがも50%上がって50%下がれば元に戻り、
50%下がって50%上がってもちゃんと元に戻る。
(exp(r)xexp(-r)=exp(r-r)=exp(0)=1=exp(-r+r)=exp(-r)xexp(r))
もちろん、連続複利で株価がマイナスになることはない。連続複利で表すものは、配当であり、
expを使う限り、配当がマイナスになることは万が一にもないのだ。(exp(r)>0)
マイナスになってはならないもの(株価や配当)を連続複利で評価するのは人類の知恵である。


ディスカッション
コメント一覧
exp(0.18 x 10^0.5 ) = 1.29
などの式がよくわからないです
大変、失礼しました。ご指摘ありがとうございました。
exp(x)とはeのx乗のことです。eとはおよそ2.718281828459045..となる数のことです。
そして、2^3とは2x2x2を表します。2^3は2の3乗(2x2x2)を表します。
つまり、exp(-0.18×10^0.5)とはおよそ2.72^(-0.18×10^0.5)のことです。
10^0.5=3.1622776601683795程度の数です。
0.18×10^0.5=0.5621…
2.7^0.5621=1.76…のことです。
2^(-3)=1/(2^3)のことです。
多分バリュエーションかと思います。
ありがとうございます。