利食いとナンピンの大きさとタイミング と 神様のイタズラ by yamamoto
効率的最適フロンティアとキャッシュ比率のお話
aというある1よりほんのすこしだけ大きな数を株価モデルに採用します。
aというのはですから、1.0001程度の数と思ってください。(1.01程度でも構いません)
そして、べき乗を考えます。a^kと書けば、これはaをk回掛け合わせたもの。
a^3ならば、a x a x a を示すものです。
このkという数字は実数(数直線上の数)を想定します。ゼロでもマイナスでも構いません。
例えば、a^-1は1/aのことです。1よりもすこしだけ小さい数です。
a^-3であれば、a^3の逆数です。1/aを3回かけたものです。
そこで、任意の株価A円が将来B円に上がったり下がったりするときに、
このAとBは数式で表すことができます。
B= A a^k - – – 1)
です。
BがAより大きいとき、株価が上がった時は、kはプラスの実数。
逆にBがAより小さいときにはkはマイナスの実数となります。
そして、BとAを結ぶkという実数が必ず存在します。
こう書くと、難しいことを言っているように思われるかもしれませんが、簡単なことです。
1)の式は、B/A = a^kと変形できます。つまり、株価がa^k倍になったということを言っているだけです。
例:2%の上昇であれば1.0001^198=1.02ですので、kは198です。
1.0001^k = 1.02を解いて、k= LN(1.02)/LN(1.0001) =198.0…
とにかく、a倍になったり1/a倍になる過程を経ながら、株価は変移していくのです。
これで株価の推移モデルが完成しました。
(宝くじと株式投資が著しく違う特性がここにあります)
宝くじはいつも300円で買えます。ところが株価が上がったら上がった部分を含めて買わないとその値段では買えません。300円の株価が3000円になったらもはや300円では買えない。宝くじとは違います。非常に大きな違いで、これを複利と言います。(一方、宝くじは単利)
どんな株価も将来はa^k倍となると表現できます。(これが複利の株価表現)
ここで、長期の上方へのドリフト率を長期投資のキャピタルゲインの年率としますが、長期では存在するドリフト率は、短期の株価推移には存在がセンシングできません。2%程度の株価の動きは、1時間程度でも生じますが、年率で10%の上昇率も1時間では10%の1/(250×5)倍になってしまうからです。250は年間営業日。5は営業日の中の営業時間です。
そこで、今回は、ドリフト率を想定しないで、a^k倍がどんな特徴を持つかを思考実験してみます。
株価は上がったり下がったりするのです。
そのため、a^k倍というkには紆余曲折があり、n-m =kとなるnとmの組み合わせが無数にあります。
何を言っているのかというと、a倍(1.0001倍)か1/a倍(1/1.0001倍)になる株価のランダムウォークが存在して、198= n-mとなるnやmが無限に組み合わせとして考えられます。一回も下がらず、最短で1.02倍になるなら、n=198,m=0の組み合わせです。あるいはn=10198でm=10000という組み合わせもあります。n-m=198になればよいのです。ずっと上がって下がってを繰り返しつつ、若干、上がるケースが多いとこうなります。
そこで、どんな株もある観察期間のうちに、上がったり下がったりするのですが、n>mならば上がり、n<mならば下がることになります。
いずれのケースでも、株価はa^(n-m)=a^k倍になるわけです。
さて、n>mのケースでは、
株価は、a^(n-m)=a^(n+0-m)=a^(n+(m-m)-m) = a^m-m x a^(n-m)
と表現できます。
B = A a^(m-m) x a^k - – – 2)
なんでこんな変形をしたかというと、ほとんどの株でnとmは細かく振動するために、大凡、同じぐらいだからです。
1%下がって、2%上がって、0.5%下がるような毎分の動きを繰り返す。
そうなると、例えば、mが150でnが200ぐらいというとなります。
トータルではすこし上がりますが、紆余曲折して行ったり来たりの部分が150あって、上昇に寄与するのはnの200の上昇のうち、50しかない。
この具体例の場合、1%下がって、2%上がって、0.5%下がるとき、
B = A a^(150-150) x a^50 =a^50ということになりますね。
B = A a^(m-m) x a^k - – – 2)
2)の式のmの大きさがかなり大きく、トータルのプロセスの中で、多くは上昇や下落に寄与しない打ち消し合いの部分となります。2)の式の右辺の積の前半a^(m-m)=1を「振動部分」と呼びます。そして、右辺の積の第2部分a^k部分は「運と実力の部分」と呼ぶことにします。
振動とは、行ったり来たり、上がったり下がったり。上がって下がってとか。下がった下がってその分上がるとか。様々な振動ですが、行ってこいの部分なので最終的に1倍。運用の成果を決するのはa^kの部分です。
多くの熟練したトレーダーは第二部分のkがプラスの数になります。
ところが、凄腕トレーダーでも運の部分が非常に大きく、運が悪いときにはkはマイナスになります。本人でさえ、運と実力の比率は厳密には分けられず、第三者から見れば、すベてがその人の実力と勘違いされるのです。
さて、何もエッジがないことがわかっている投資初心者の場合、kの項は、ほぼ、運が支配することになります。運の支配するa^kの部分を無視して、第一の振動部分であるa^(m-m) =1の部分を分析することで最適な効率的フロンティが求められます。
え? 1倍がそんなに重要なの?と読者は思うかもしれませんが、1倍がすべての投資の基本式です。
1倍とは、1 = a^0 = a^(m-m) = a^m x (1/a)^mです。(n>m)
(n<mの場合は、mをnに取り替えると同じ議論が成り立つ)
そして、1倍とは連続複利で0%です。(LN(1)=0)
ここで、投資ウエイトwという係数を導入します。wは0以上の実数です。
w=1がフル投資でキャシュを残さず投資した場合。
w=0.5が株式半分でキャッシュが半分の場合。
w=3は、信用取引で元手の2倍を借金した場合。
係数wを加味した1倍の振動の投資の結果は、こうなります。
(wa +(1-w))^m(w/a +(1-w))^m - – – 3)
3)式の1-wの部分は、キャッシュ部分ですので、相場変動と無関係で不変です。
w=3のとき、信用取引のフルフルの状態ですが、aを3倍にする成果が得られるか、失敗した時のw/a倍になるかです。
3)は[(wa + (1-w))(w/a + (1-w))]^mですので、
この[…]の中、(wa + (1-w))(w/a +(1-w))の中身が1より大きいか小さいかが非常に問題になります。
この中身が1より小さい時、繰り返しのべきm乗で、取引をすればするほど、全体はゼロになってしまうからです。
つまり、投資家は破産してしまうからです。
(wa + (1-w))(w/a +(1-w))をwの二次式とみなした場合、
このwの二次式は、上に凸の最大値を持ちます。
何故ならば、wの二乗の項の係数がマイナスになるからです。
(時間のある方は中学生の問題ですので、展開して確認ください)
(a+1/aが作り方から2より大きくなるため… a>1であるから)
a>1ですので、a-1>0ですね。(a-1)(a-1)>0が成り立ちます。(a-1>0なので))
すると、a^2+1 > 2aですから、1より大きな数aで不等式の両側を割るとa+1/a >2となるのでした。
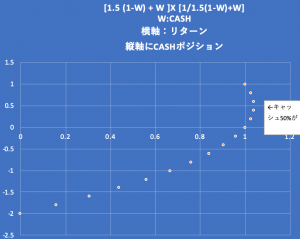
さて、この二次式をwで微分して、微分が0になるwがこの2次式の最大値です。そして、wで微分して0となる点は、w=0.5です。
果たして、w=0.5のとき、恒常的に上記二次式は1より大きくなります。
つまり、上がって下がって上がって下がってと同数の行ったり来たりの繰り返して儲かることになります。
ところが、wが1を超えると上記二次式は1よりも小さくなります。
それが信用取引が運が悪いと借金を背負うということ以上に、効率的最適フロンティアを大きく逸脱しているためのリスクリターンの比率が極端に悪いということの演繹的な証明になります。
w=3のとき、上記二次式は13-6(a+1/a)ですが、a+1/aが2より大きな数ですので、13-12.xxxですから結果は1を下回ります。
これを数百回も行えば、大きな投資損失となります。
このように、振動を利用して取引を多くのトレーダーが行なっていますが、
2)式をトレードの第一部分(振動)と第二部分(運と実力の部分)と分けた時、
第二部分の運と実力を信じる部分でトレーダーはトレードを決断します。
しかし、本来は、自動的に振動する部分が多い株を選んで、細かく振動を取ってキャッシュ・ウエイトを絶えず1/2に微調整していく操作さえできれば、確実な利益となります。w=1/2を連続時間で維持することは実務的には難しいことですが、ヘッジファンドでは可能になります。それでも第2部分の運と実力の要素がいたずらをするため、確定したリターンは得られません。また、取引コストや税金がかかることなどを考えれば、実用には程遠いと思われます。それはそうと、w>1の信用取引は非常に不利になる、これが今回の結論です。
皆様は、おかしい。キャッシュは持ちつつ、株価がだけが行ってこいになるなら投資は1のままではないかと思われるかもしれませんが、誤解です。複利とは常識が通用しない現象なのです。[aw+(1-w)]^nは絶えず変化して大きくなります。その大きさに合わせてキャッシュポジションも大きくする作業(すなわち株を少し売る作業)をするのが振動部分においては最適な複利運用なのです。(宝くじと違う株投資の本質的な特徴)
効率的有効フロンティアとは、リターンとリスクの関係を最大化するポートフォリオの最適構成です。
今の話は、振動部分のみの話です。もちろん、運と実力の項である、a^k=a^(n-m)が投資の本質的な部分であり、長期投資というのは、長期投資だけが利用できる銘柄の選択効果を狙って、年率10%程度の株価の上昇ドリフト率を利用して、kをプラスにする戦略です。
この場合、最初の第1部分の振動は利用しません。キャッシュ半分では年率で数%のリターンの機会損失となるためです。振動という短期を利用するデイのトレーダーであれば、キャッシュポジションは必須です。これは演繹的な数の世界からの結論であり、単なる経験則とは違うのです。
考えて見れば当たり前の話ですが、ここに50株で50がキャッシュの投資家がいて、株が60に値上がりするとキャッシュは50のままですから、トータルのポートフォリオは110に増えます。キャッシュ比率50%を保とうとすれば値上がり益10を売るのではなく、5だけを売る。逆に株価が40に下がってしまったら、キャッシュ5の部分を株にシフトする。そうなると、全体は90ですが株45とキャッシュ45で釣り合う。これを繰り返すということは、つまり、下がったら買い、上がったら売りを繰り返すので儲かる。ところが、神様はいたずらをする。慌てるなになにはもらいが少ないように神様が操作するのです。同じ振動現象を与えても、レバレッジ取引、信用取引をする人には、振動すればするほど損するようになっている。そうしないと、楽して儲ける人ばかりになって、人類が滅亡してしまうからです。逆説的に言えば、真っ当な努力、無理しないシステムで生きている人を神様は応援する。時間を買う人々に対しては神様は不利益を与えるということです。
最適ウエイトへの調整は必然的に利食いとナンピンという行為になります。
上がれば利食い、下がればナンピン。それを繰り返すとき、最適投資ウエイトw=1/2だけ株を残すことになります。
エッジのない投資初心者の場合、キャッシュ比率50%を固定した[デルタヘッジ]をすることで利益を得ることができます。
w=0.5を残すという原則では、株価の上昇部分の半分の利食い。ナンピンは下落した部分の半分のナンピンということになります。
株価が10%下落した時に、5%だけキャッシュを使ってナンピンする。それが最適なポートフォリオを保つリバランスとなります。
これは運用の現場や投資家の実際からは大きく離れた結果だと思われます。多くはナンピンの量もタイミングも非常に大きくダイナミックです。利食いも思い切りの利食いが多い。これは投資家がポートフォリオ運用をしていないことの裏返しです。投資家の多くは、個別のトレードの成否ばかりに目がいっているのです。
もちろん、投資というのは個別トレードの集合体とみる考えがトレーダーやディーラー中心に存在するのは承知しています。ファンドマネジャーである私は、投資を個別トレードの集合体はまったく見なさないのです。そんなことをすればトータルで負けてしまうからです。つまり、全部勝とうとしてトータルで負けてしまう。これがポートフォリオ理論を知らないディーラーの負ける典型的なパターンです。
個々のトレードのことをあまり考えず、ポートフォリオを一つの商品として見るのがファンドマネジャーです。その立場では、商品性を保つためのリバランスにおいて、ナンピンも利食いも非常に小さな割合と小さなインパクトで行うのが実際の実務になります。個別のトレードでわざと負ける時も多いのです。ただし、こちらは、トータルとして結果で勝つことを優先しているので、ファンドをマネッジできるのです。
もちろん、振動するだけの株というものはなく、多くは上昇トレンドと下落トレンドにあります。a^kで運と実力の部分を試すならば、長期の視点で自然な上方ドリフト率を活用するのがよいでしょう。利益率が高い、長期のトレンドで年足が過去10年中8年で陽線であればよいし、長期の二点間の株価のドリフト率が年率で二桁以上あれば合格です。それを単品勝負ではなくて、ポートフォリオとして組み、ポートフォリオとして最小分散を実現する利食いとナンピンを繰り返すのがポートフォリオ運用です。ご興味がある方は、共分散行列を各銘柄のウエイト付きでじっと眺めてください。どこをどうすればよいのか、きっとわかるはずです。各銘柄のウエイトを動かしたの行列ノルムの最小点が存在し、そのウエイトを維持するのが運用の第一歩です。


ディスカッション
コメント一覧
まだ、コメントがありません