理論株価クイズ007 -ギャンブルで遊んで暮らす方法-
理論株価クイズ007 -ギャンブルで遊んで暮らす方法
大学四年のひろし君は就職活動もしないでギャンブルで暮らそうと計画を立てています。というのも、とんでもなく有利なギャンブル場が開設されることがわかったのです。規制緩和で大阪にカジノができるのです! カジノにはマルチンゲールというゲームがありハウスとひろし君との1:1の勝負をします。双方チップ1枚を出します。丁半博打をします。テーブルのチップはハウスかひろし君かどちらか勝ったものがいただくのです。負けた相手はゲームを続ける権利があり、勝った相手もそれを受ける義務があります。次に双方2枚のチップを出します。テーブルのチップは勝った方が総取りします。ここまでで負けた方は3枚のチップを出していますが、この勝負に勝てばテーブルには4枚のチップがありますので、トータルでは一枚チップ分だけ得ることができます。このゲームをN回続けていけば、初回2^0チップ、2回目2^1のチップ、N回目は2^(N-1)のチップが必要となります。しかし、勝った方の利益はチップ一枚です。負けが込んだ相手がギブアップするまで勝負が続きます。(チップは1枚で1万円)
(2^Nとは2のN乗のことです)
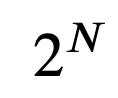
(1/2^Nとは1/2のN乗のことです) 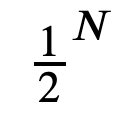
これをここでは、マルチンゲール戦略と呼ぶことにします。
ひろし君は回を重ねるごとに上がる勝率に着目しました。これって絶対勝つじゃん!! 何故ならば丁半博打の勝率は5割。1/2です。負けても負けても次に挑めばいつかは勝てるだろう。するとN回の勝負で全部負ける確率が1/2^Nですから、99%勝てる回数は、(1/2)^N<0.01 を計算すれば出せます。要は2^(N-1)の数だけのチップがあれば99%勝てるのだ。チップ一枚が10000円ならば、毎日賭博を一回するだけでなんとか就職しなくても良さそうです。
ひろしくんのギャンブルで暮らす大作戦は成功するでしょうか?
理論株価クイズ007 -マルチンゲール-
クイズです。マルチンゲール戦略をとります。
A) なるほど!そんな良い方法があったのか。ひろし君は成功する。頑張って。
B) いいえ。この作戦はナンピンと同じ。非常に危険です。やめた方が良い
確率と期待値とリスクと
ひろし君は今からでも遅くありません。リスクとリターンが見合わないことを計算してみるべきです。99%って1%も失敗する作戦では投機をデザインしたことにはなりません。投資であろうが投機であろうが、全ては「デザイン」が大事です。デザインのない投資よりはデザインのある投機の方がよっぽど良いのです。
毎日賭博をするというデザインで1%の確率の負けは、どんな頻度で起こるでしょう?
100日あれば1日ぐらい負けると想定すれば良いでしょう。負ける確率は1%なのですから。
もちろん正確にいつ負けるかはわかりません。運よく200日勝ちを続けることもあるかもしれませんし、100日で負けるかもしれません。10日後に負けるかもしれません。こんなとき、負けの最もあり得る予想は何日後でしょうか。一時間に一本のバスを待つとき最長で1時間待てば良いので平均的にはその半分の30分が期待される待ち時間です。つまり100日に1回、負けがくるのであれば50日後に負けると想定しなければならないでしょう。
ひろし君は初日から負けるまで、49連勝するとしましょう。チップ49枚をゲットしている状態です。そして、初めて負けます。50日目のことです。ハウスに巻き上げられるチップは2^(N-1)でした。このNを求めてください。99%の勝率を確保するためには1/2^N<1/100となるNですから、N x LN(1/2)=LN(1/100)からN>6.64となります。
Nは自然数ですから、N=6では勝率99%になりません。そこでN=7で2^N-1=2^7-1=127枚がひろし君が用意しなければならないチップ総数(元手)です。(N=7で勝率は99.2%)
さて、50日目あたりで127のチップを全て出して、勝負に挑んだひろし君ですが、万に一つではなく百に一つの確率で負けてしまいます。失うチップは127です。ここでゲームオーバー。気分は大負けですっからかんです。(正確には元手127万円の過半を失って茫然自失状態)
手順としてはNを先に計算して、勝率をNから99.2%と出してから、期待される負けの日を一様分布で想定して通算の損益を出す、という手順の方が良いですね。私は先に想定勝率(デザイン)から出してしまったのですが、まあ、誤差ということでご勘弁ください。ひろし君の計画は破綻するでしょう。通算損益は49のプラスに127のマイナスで赤字。いつかはハウスにやられます。ハウスを超える膨大な資金が必要となります。勝率が高くても負けのインパクトがすごいのでこの戦法は期待値が低いのです。マルチンゲール戦略と呼ばれる戦法で、ナンピンの信者からは支持されます。ナンピンやマルチンゲールは勝率は回数を増やせば高まりますが、ゲーム自体の期待値を上げることはできません。
Nを大きくする意味はあるのか? 勝率99.999%ならやる意味はあるのか?
自分のことだけを考えるのであれば、一様分布の負けの日を100年以上に設定しなければなりません。寿命を超えて負けが来る=負けないと投機をデザインするのです。36500日負けないためには、その倍の73000日。つまり73000日に一回の負けを想定することからデザインすれば良いでしょう。1/73000 > 1/2^NとなるNを計算してください。16.15ですが、おまけでN=16として良いでしょう。多分、大丈夫。ダメなら生きている間に破産です。怖い設計ですね。65536(=2^16)ものチップが用意できれば良い。チップは1万円ですから、6.5億円の資産を用意しないとマルチンゲール戦略では破産ですね。N=17とすれば死ぬまで負けることはないはずですが、確約はできません。その場合は13億円ご用意ください。
馬鹿馬鹿しいゲームです。期待値がどんなに大きなリスクとなっても勝ってもリターンはチップ1枚のままです。期待値はカジノの入場料の分だけマイナスです。リスクは非常に高い。実際、6.5億円の元手を用意して得られるリターンが年で365万円ならば利回り0.6%です。リスクは6億円が全部パーになること。ああ、ナンピンは怖いですね。
期待値はゼロとなることを確認ください。しかし、実際は、一回の負けでゲームオーバーとなるため、計算上の期待値と結果が大きく変わります。これをリスクと呼びます。このクイズの答えはBです。この戦略は危険すぎます。
ひろし君の模索は続きます。就職しない、遊んで暮らせる方法は見つかるでしょうか?頑張れ!ひろし君!


ディスカッション
コメント一覧
まだ、コメントがありません